Number System - Notes

Numbers are the basic tools of Mathematics. A Number System is a way of representing and expressing numbers using a set of symbols and rules. The study of the number system enables us to classify numbers into distinct groups and comprehend their properties.

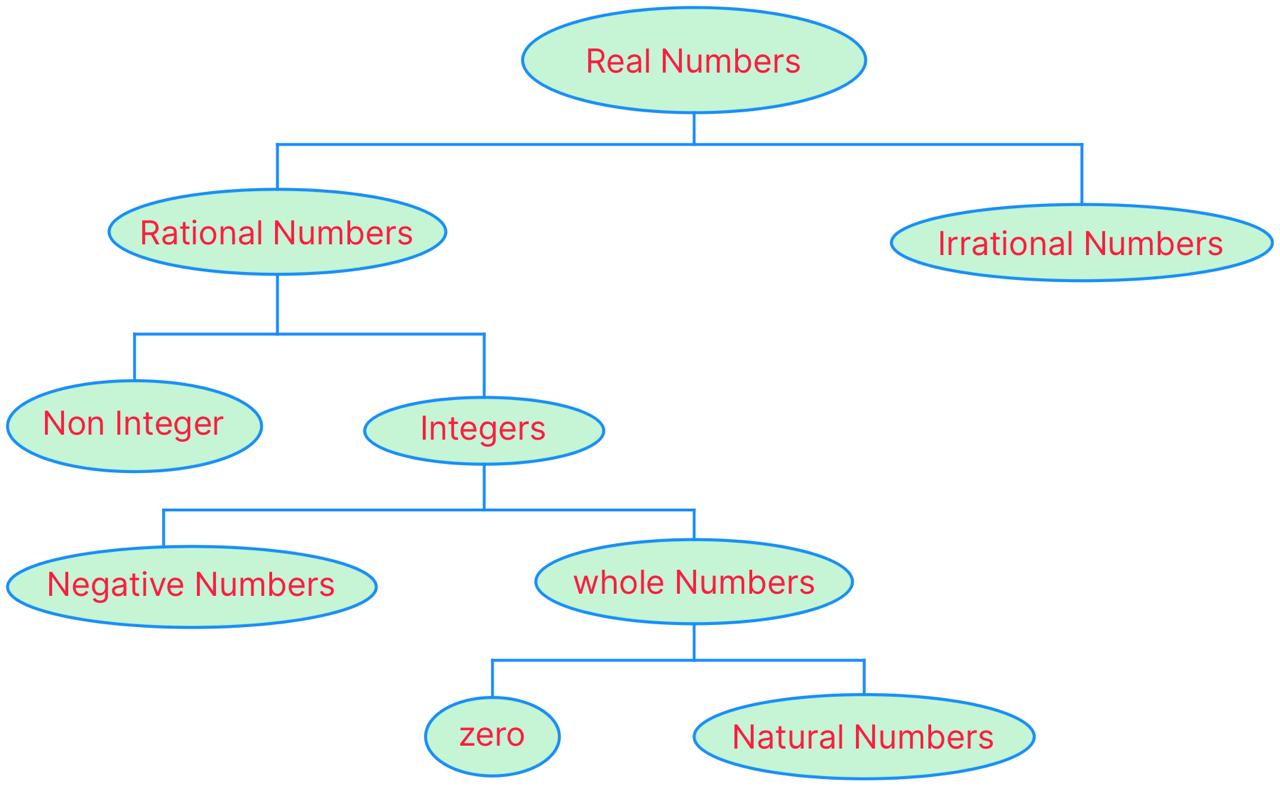
In mathematics, numbers are broadly divided into:

• Natural Numbers \(\mathbb{(N)}\): Counting numbers starting from 1, 2, 3, …
• Whole Numbers \(\mathbb{(W)}\): All natural numbers along with 0.
• Integers \(\mathbb{(Z)}\): All whole numbers and their negatives (…, -3, -2, -1, 0, 1, 2, 3, …).
• Rational Numbers \(\mathbb{(Q)}\): Numbers that can be written in the form p/q, where p and q are integers and q ≠ 0.
• Irrational Numbers: Numbers that cannot be written in the form p/q (like √2, π, etc.).
• Real Numbers \(\mathbb{(R)}\): The set of all rational and irrational numbers.

• Definition: The numbers that we use for counting objects are called Natural Numbers. Example: 1, 2, 3, 4, 5, …
• Symbol: The set of natural numbers is denoted by \((\mathbb{N})\).

\[\mathbb{N} = \left\{1,2,3,4,5,\cdots\right\}\]

• Important Points:
  • Natural numbers start from 1 and go on endlessly.
  • 0 is not a natural number.
  • Every natural number has a successor (next number), but no natural number has a predecessor (previous number).

whole number is a number without fractions or decimals. It includes 0 and all natural numbers (1, 2, 3, 4, …).

In short:

• Whole Numbers \(\mathbb{(W)}\) = {0, 1, 2, 3, 4, …}
• They do not include negative numbers, fractions, or decimals.

An Integer is a number that can be positive, negative, or zero, but it cannot be a fraction or a decimal.
Set of integers: \[\scriptsize Integers \mathbb{(Z)}=\left\{\cdots, -3, -2, -1, 0, 1, 2, 3,\cdots \right\}\]

Key Points:

• Positive Integers: 1, 2, 3, 4, …
• Negative Integers: -1, -2, -3, -4, …
• Zero (0) is also an integer.

Rational Number\(\mathbb{(Q)}\)

The collection of rational numbers is denoted by \(\mathbb{Q}\).
‘Rational’ comes from the word ‘ratio’, and Q comes from the word ‘quotient’.
A number ‘r’ is called a rational number if it can be written in the form \(\frac{p}{q}\), where p and q are integers and \(q \neq 0\).
Examples:
Fractions: \(\frac{1}{2}, \frac{-3}{4}, \frac{5}{1}\)
Integers: (since they can be written as \(\frac{n}{1})\): -3, 0, 5
Repeating Decimals: \(0.333\cdots = \frac{1}{3}, 0.142857\cdots\frac{1}{7}\)

Terminating Decimals: \(0.5 = \frac{1}{2}, 1.25 = \frac{5}{4}\)
Key Points:

• All integers are rational numbers.
• Every terminating or repeating decimal is a rational number.
• Denominator can never be zero.

Note: There are infinitely many rational
numbers between any two given rational numbers

An irrational number is a real number that cannot be expressed as a ratio of two integers; it cannot be written in the form \(\frac{p}{q}\), where p and q are integers and \(q\neq 0\).
Key Features of Irrational Numbers: Their decimal expansion is non-terminating and non-repeating.

• They cannot be expressed as fractions of integers.
• They lie on the number line just like rational numbers, but they “fill the gaps” left by rationals

Examples:

• \(\pi = 3.141592\cdots\) (non-repeating, non-terminating)
• \(\sqrt{2} = 1.414213\cdots\)
• \(e=2.718281\cdots\)

Together, rational and irrational numbers form the set of real numbers \(\mathbb{(R)}\)

1. A number r is called a rational number, if it can be written in the form \(\frac{p}{q}\) , where p and q are integers and (qne 0).
2. A number s is called a irrational number, if it cannot be written in the form (frac{p}{q}), where p and q are integers and \(q\ne 0).
3. All the rational and irrational numbers make up the collection of real numbers.
4. If r is rational and s is irrational, then r + s and r – s are irrational numbers, and rs and \(\frac{r}{s}\) are irrational numbers, \(r\ne 0\).
5. For positive real numbers a & b, the following identities holds:
   • \(\sqrt{ab}=\sqrt{a}\sqrt{b}\)
   • \(\sqrt{a\over b}={\sqrt{a}\over \sqrt{b}}\)
   • \((\sqrt{a} + \sqrt{b}) - (\sqrt{a} - \sqrt{b})=a-b\)
   • \((a + \sqrt{b})(a - \sqrt{b})=a^2 - b\)
   • \((\sqrt{a} + \sqrt{b})^2 = a + 2\sqrt{ab} +b\)
6. To Rationalize the Denominator of \(\frac{1}{\sqrt{a} +b}\), we multiply this by \(\frac{\sqrt{a} -b}{\sqrt{a} -b}\) where a & b are integers.
7. Let (agt 0) be real number and p and q be rational number then
   • \(a^p . a^p = a^{(p+q)}\)
   • \({(a^p)}^q = a^{pq}\)
   • \(\frac{a^p}{a^q}=a^{p-q}\)
   • \(a^p . b^p = (ab)^p\)
8. The decimal expansion of a rational number is either terminating or nonterminating recurring. Moreover, a number whose decimal expansion is terminating or non-terminating recurring is rational.
9. The decimal expansion of an irrational number is non-terminating non-recurring. Moreover, a number whose decimal expansion is non-terminating non-recurring is irrational.